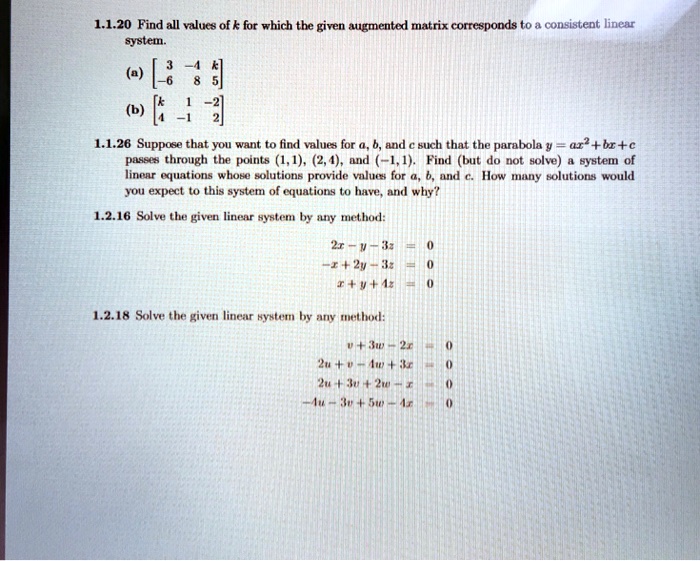
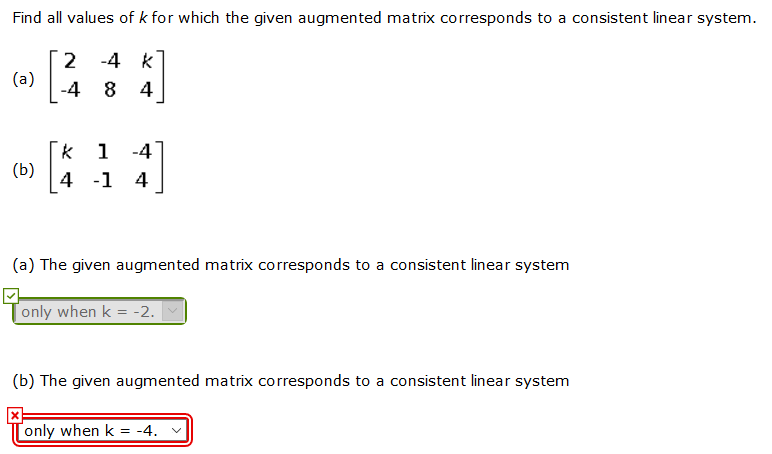
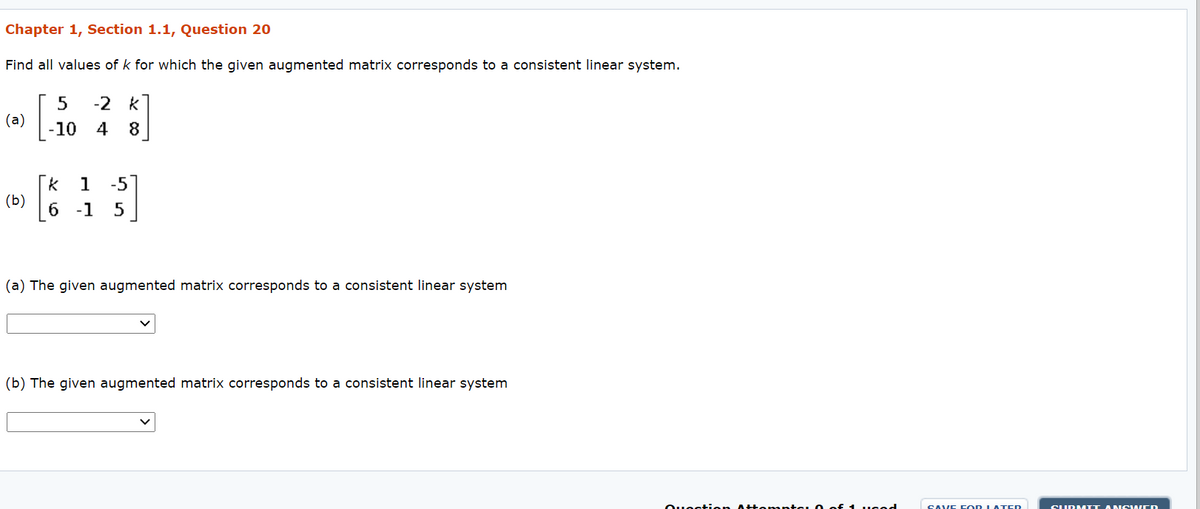
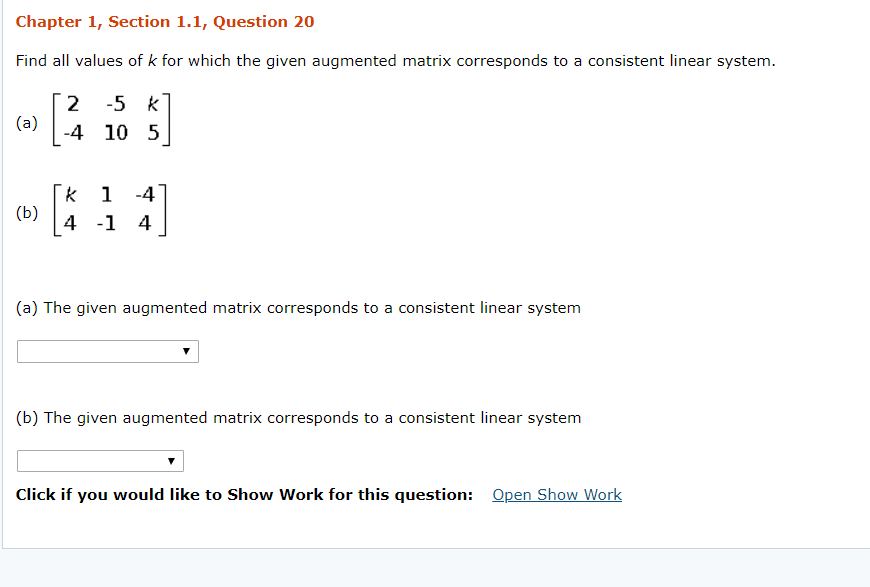
For What Value(s) Of K Is The Linear System Consistent?
For what value(s) of k is the linear system consistent?. It has no solution if and only if a 1 a 2 b 1 b 2 c 1 c 2. System is consistent for all value of k except. Here the system of equation is.
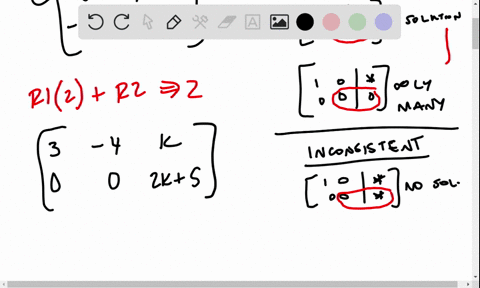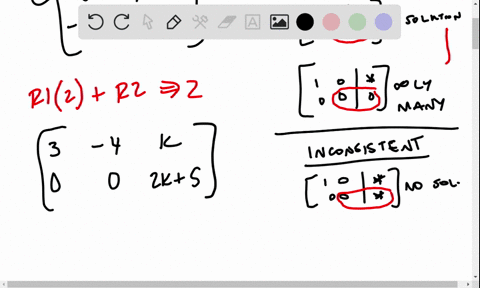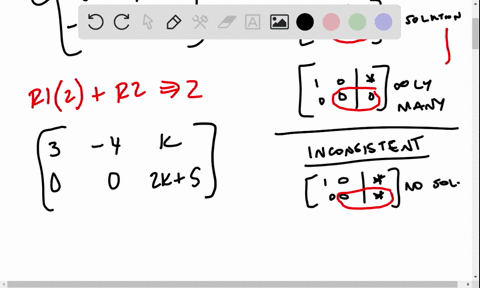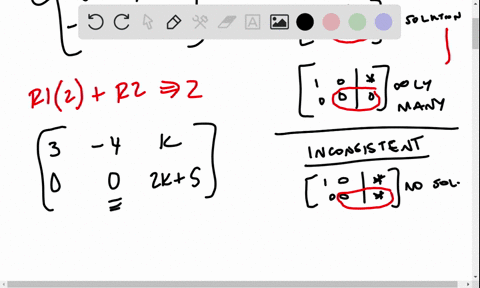
B The augmented matrix of the given system is 4 6 10 6 9 15 Divide the first row by 4 to obtain 1 3 2 5 2 6 9 15 Now add to the second row 6 times the first row to obtain 1 3 2 5 2 0 0 0 Hence x 2 s is a free variable. When the determinant is 0 the two lines are guaranteed parallel but not necessarily overlapping. In this video I show you how to solve for K when the system is consistent.
The given system is consistent when determinant of A is not equal to zero. And were keeping track of whats happening to the variables on the right. For a system to be consistent the ratio of coefficient of x terms and y terms should not be equal that is.
We have been given a system of equations as. Consider a linear system whose augmented matrix is first row 1 1 2 0 second row 1 2 -3 -1 third row 9 19 k -9 For what value of k will the system have no solutions. Since this is a fairly simple system however you could easily pick a value of k which causes.
The system is dependent has infinite solutions when k2. In the above two cases the system is consistent. 2 5 x 7 y 15 x k y 3.
We must find the value of k such that the system is consistent. Since the given system will be consistent for all value except therefore we can choose any values for k such as or 2. I give you the basic of what consistent and inconcosistent systems are.
100 4 ratings for this solution. Chapter 3R Problem 8CT is solved.
The given system is consistent when determinant of A is not equal to zero.
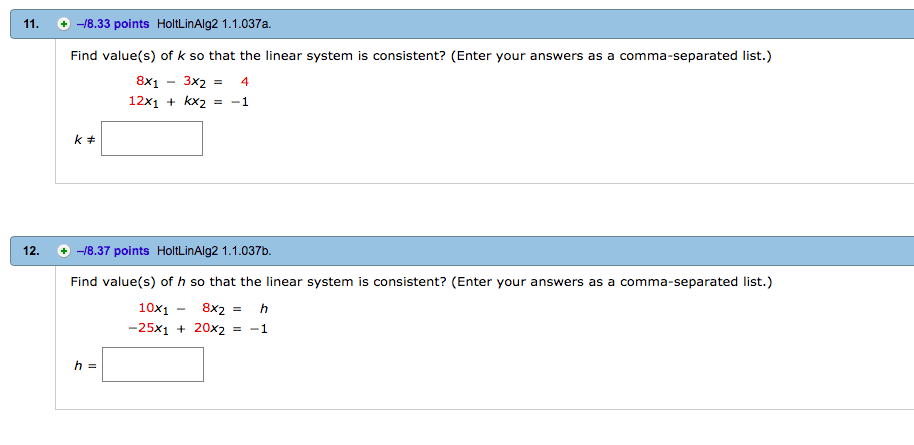
B The augmented matrix of the given system is 4 6 10 6 9 15 Divide the first row by 4 to obtain 1 3 2 5 2 6 9 15 Now add to the second row 6 times the first row to obtain 1 3 2 5 2 0 0 0 Hence x 2 s is a free variable. I give you the basic of what consistent and inconcosistent systems are. So for this problem were asked to find the values of G H and K that will make this system consistent. The given system is can be represented by. Hence a linear system with corresponding augmented matrix. Since this is a fairly simple system however you could easily pick a value of k which causes. 2 5 x 7 y 15 x k y 3. In the above two cases the system is consistent. For a system to be consistent the ratio of coefficient of x terms and y terms should not be equal that is.
System is consistent for all value of k except. The most direct way to declare that a system is inconsistent is by looking for the value of k which causes the determinant of the matrix to be zero. 4k6k13 This system of linear equations can have infinite solutions only if the determinant of the 2xx2 matrix 4kk1 is 0. Since the given system will be consistent for all value except therefore we can choose any values for k such as or 2. In the above case the system is inconsistent. Chapter 3R Problem 8CT is solved. Therefore for all k the system is consistent.




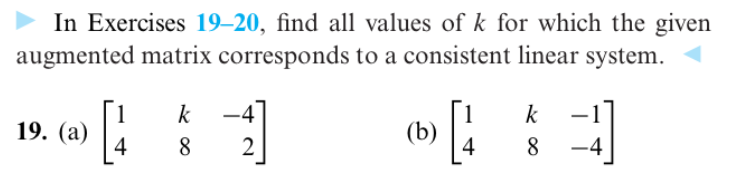






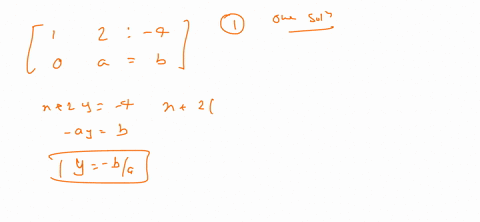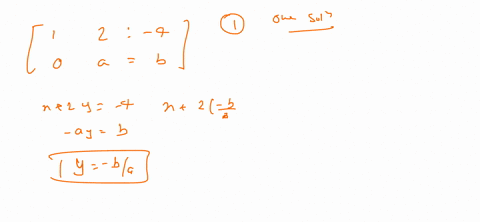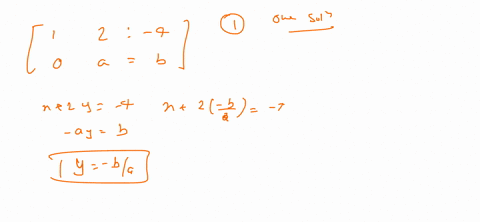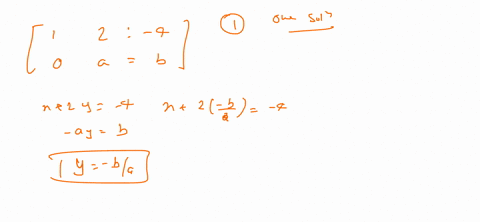




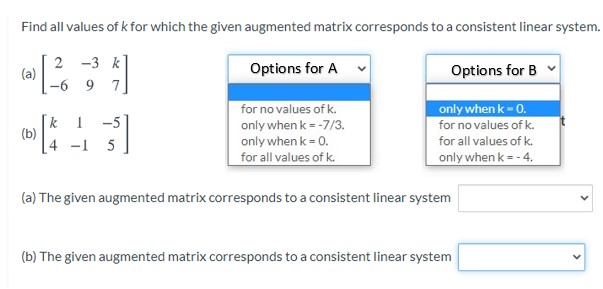







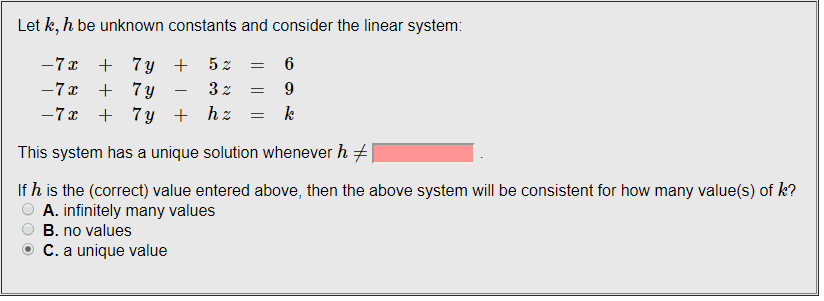
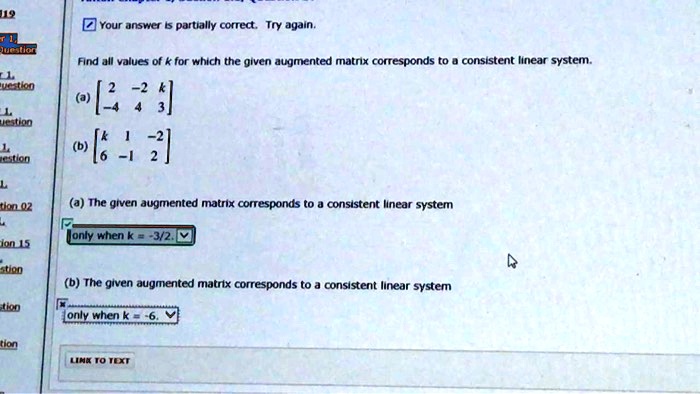






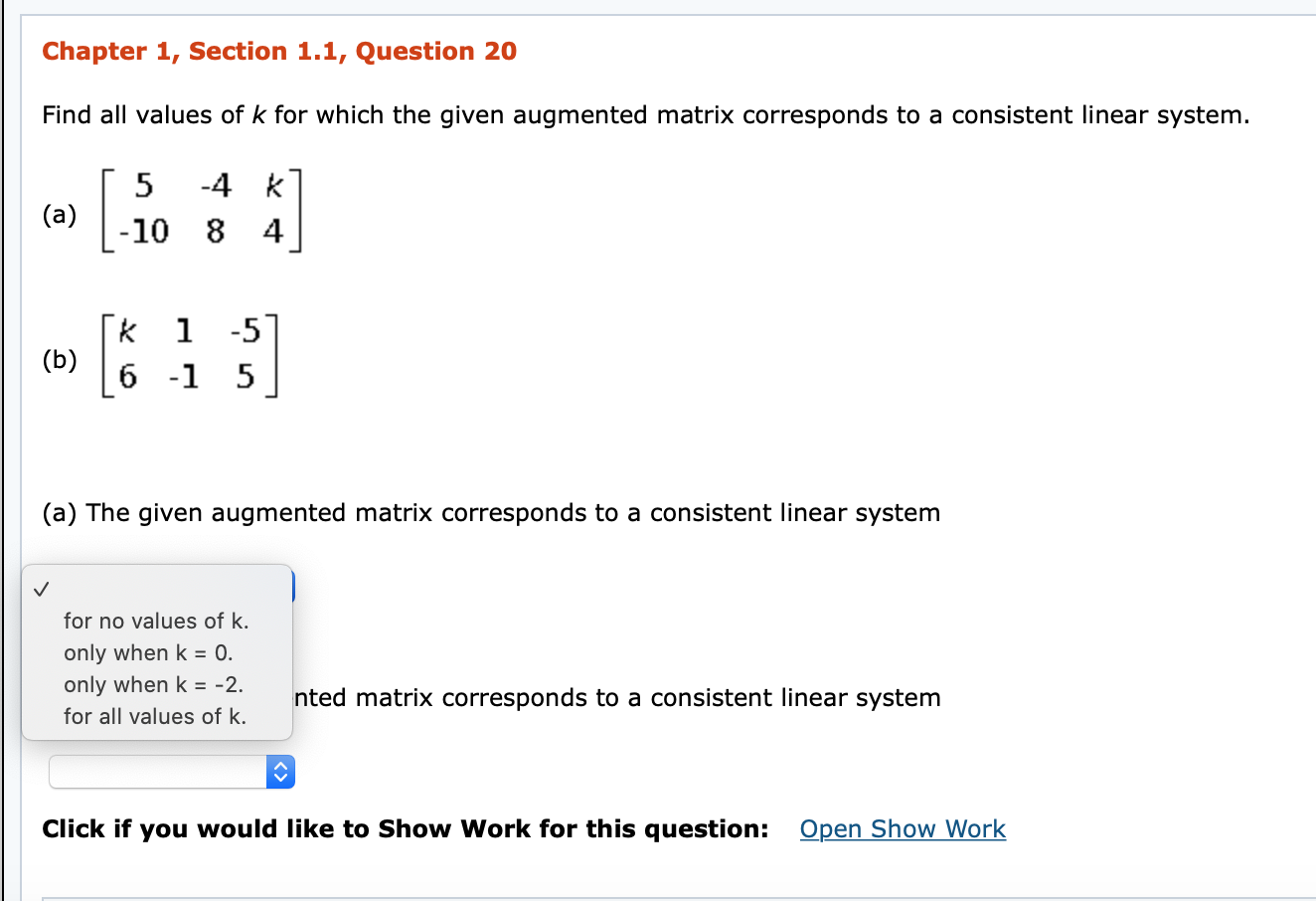
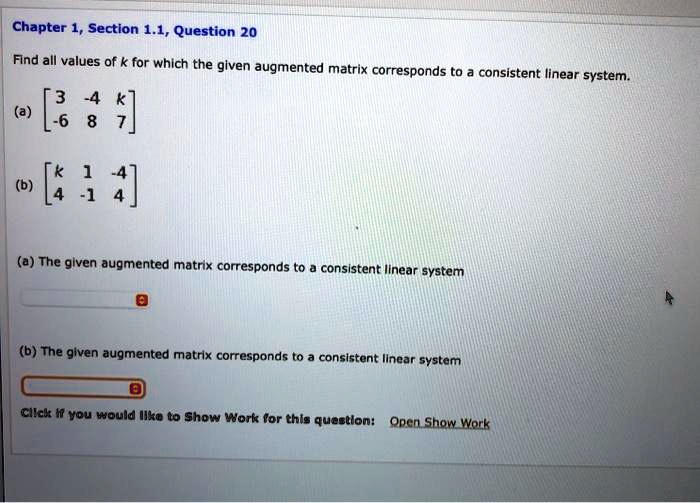


Post a Comment for "For What Value(s) Of K Is The Linear System Consistent?"